Correlation

Information

Correlation means how well thee data fits to a straight line (e.g.How close data points are to the LOBF [Line of Best Fit])

If the data fits to a curve do not use the product moment correlation coefficient r as we are only checking for a straight line

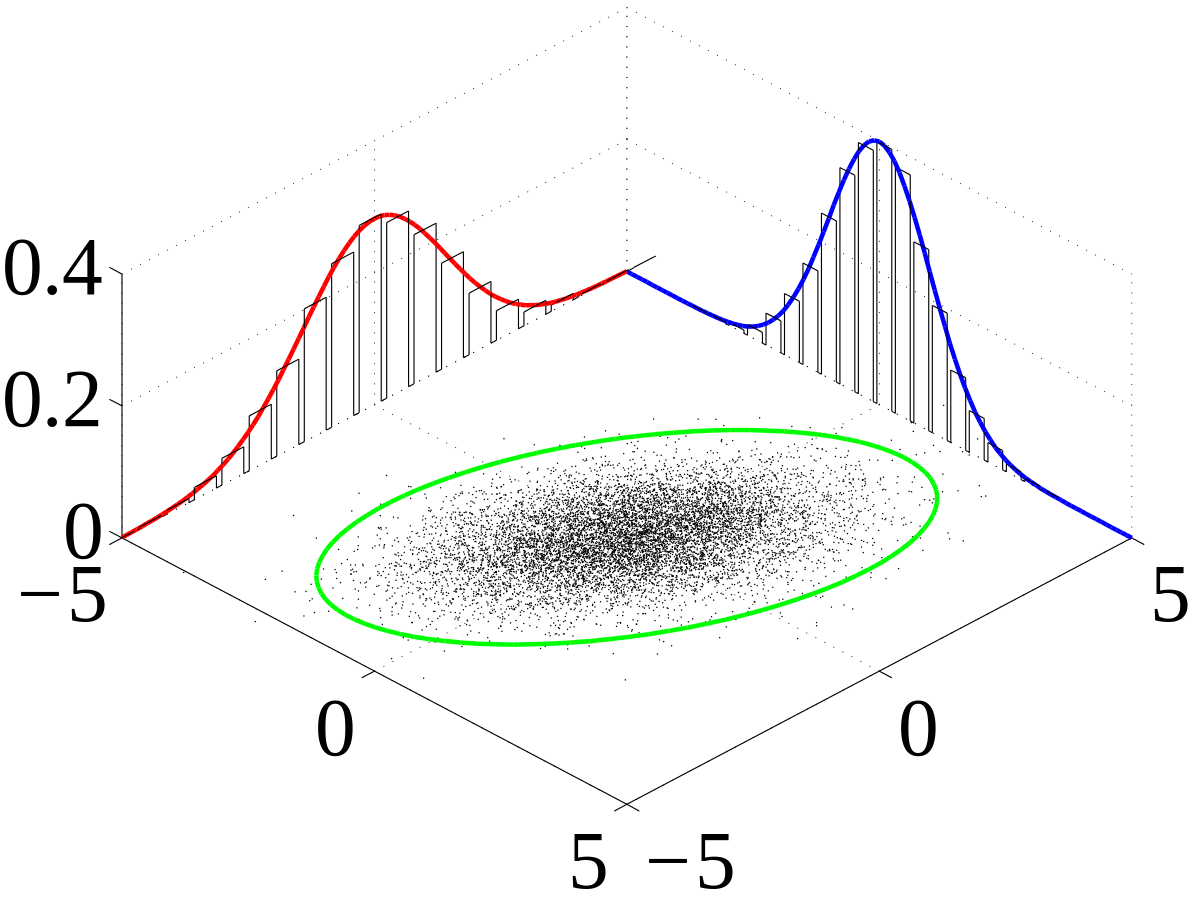
In order for correlation to work data must be jointly normally distributed this means that the majority of all data is centered around the mean as shown in the diagram below where for variable x and y most data is focused around the central point and then as you are further from the mean there are less data points
(Graphs shows amount of data points againt variable)

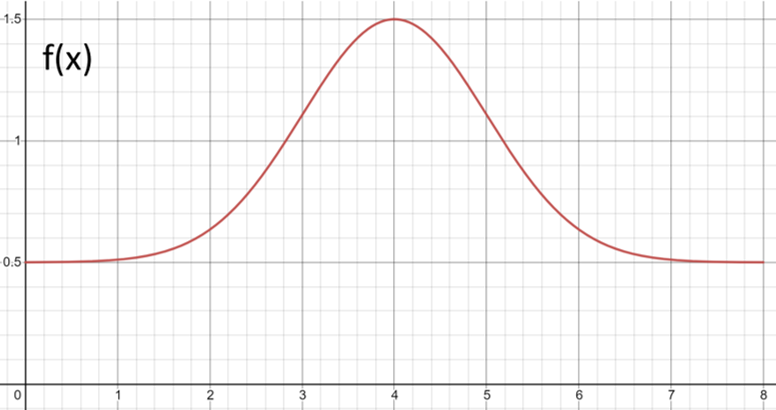
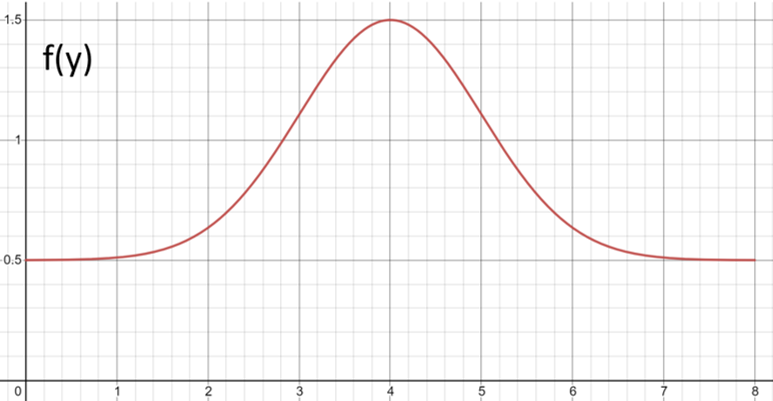
Combining these two graphs into a 3-D graph we can see that all data points are centred about one point as shown in the graph below

In order to find the value for r (product moment correlation coefficient) we must use this equation:

$$r = \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}}$$

From previous knowledge we know how to find two of these values but as they are so important we will show you there equation once more:
(Where n is the number of data point)

$$S_{xx} = \sum{(x-\bar{x})^2} ≡ \sum{x^2} - \frac{(\sum{x})^2}{n}$$

$$S_{yy} = \sum{(y-\bar{y})^2} ≡ \sum{y^2} - \frac{(\sum{y})^2}{n}$$

$$S_{xy} = \sum{(x-\bar{x})(y-\bar{y})} ≡ \sum{xy} - \frac{(\sum{x})(\sum{y})}{n}$$

We can represent r on a scale to correspond its value to how we would see the correlation on a graph like so:

-1.0	-0.5	0	+0.5	+1
Perfect Negative Correlation	Moderate Negative Correlation	No Correlation	Moderate Positive Correlation	Perfect Positive Correlation

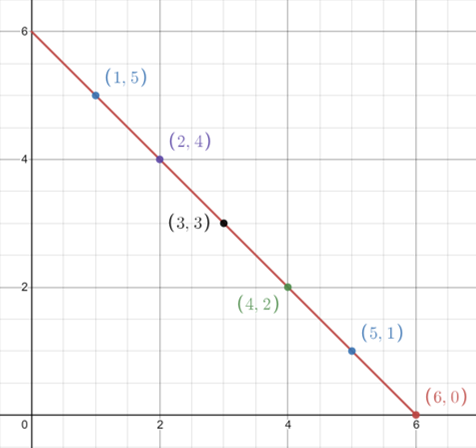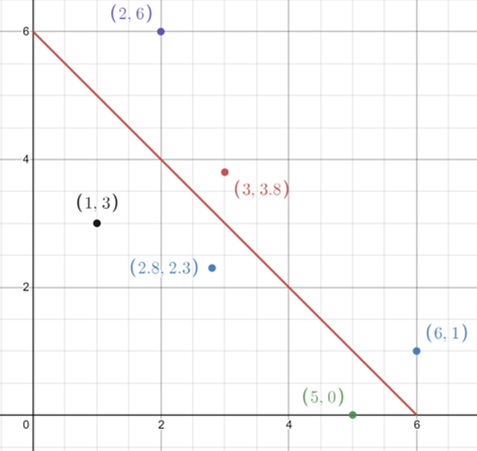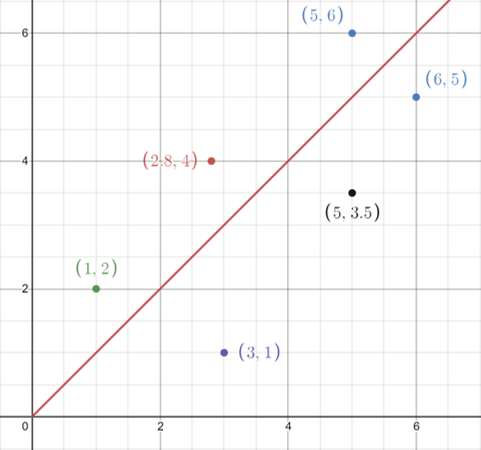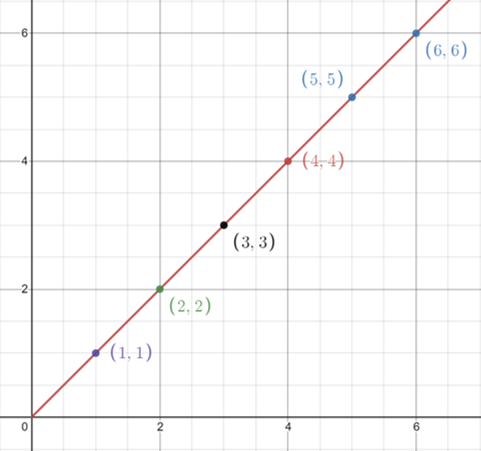Product Moment Correlation Coefficient (r)

Now let us show an example of finding the Product Moment Correlation Coefficient (r)

Example 1

Given the data points:

x	y	$$x²$$	$$y²$$	xy
5	240	25	57600	1200
5	232	25	53824	1160
7	227	49	51529	1589
8	222	64	49284	1776
10	215	100	46225	2150

$$n = 8$$

$$\sum{x} = 35$$

$$\sum{y} = 1136$$

$$\sum{x^2} = 263$$

$$\sum{y^2} = 258462$$

$$\sum{xy} = 7875$$

$$S_{xy} = \sum{xy} - \frac{(\sum{x})(\sum{y})}{n} = 7875 - \frac{35×1136}{5} = -77$$

$$S_{xx} = \sum{x^2} - \frac{(\sum{x})^2}{n} = 263 - \frac{35^2}{5} = 18$$

$$S_{yy} = \sum{y^2} - \frac{(\sum{y})^2}{n} = 258462 - \frac{1136^2}{5} = 362.8$$

$$r = \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}} = \frac{-77}{\sqrt{18×362.8}} = -0.953$$

This means thats these two data sets have a very strong negative correlation

Example 2

x	y
4	8
10	6
9	10
7	5
6	8
5	4
7	8
9	9
8	7
6	4

$$n = 10$$

$$\sum{x} = 71$$

$$\sum{y} = 69$$

$$\sum{x^2} = 537$$

$$\sum{y^2} = 515$$

$$\sum{xy} = 502$$

$$S_{xy} = \sum{xy} - \frac{(\sum{x})(\sum{y})}{n} = 502 - \frac{71×69}{10} = 12.1$$

$$S_{xx} = \sum{x^2} - \frac{(\sum{x})^2}{n} = 537 - \frac{71^2}{10} = 32.9$$

$$S_{yy} = \sum{y^2} - \frac{(\sum{y})^2}{n} = 515 - \frac{69^2}{10} = 38.9$$

$$r = \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}} = \frac{12.1}{\sqrt{32.9×38.9}} = 0.338$$

This means thats these two data sets have a weak positive correlation

Example 3

Knowing that the values for x represent the head and body length of doormice and that the values for y represent the tail length of doormice and are recorded in metres
Finally given the information that:

$$S_{xy} = 416.3,$$

$$S_{xx} = 1280.55,$$

$$S_{yy} = 282.8$$

Part a

Calculate the value of the product moment correlation coefficient between x and y

$$r = \frac{S_{xy}}{\sqrt{S_{xx}S_{yy}}} = \frac{416.3}{\sqrt{1280.55×282.8}} = 0.69$$

Part b

Interpret the r value in the context of this question

From the r value we can see that there is a moderate positive correlation between 'head and body length' and the 'tail length' of doormice

Part c

Write down the value of the product moment correlation coefficient if the measurement had been recorded in centimetres

The 'pmcc' would still be 0.692, since a change of units has no effect on the calculation

Part d

Why is it not generally advisible to calculate the value of 'pmcc' without first viewing a scatter diagram of the data. Illistrate answer with the use of a sketch

Three reasons that it would be a good idea to first draw a sketch is the existance of:
Outliers
Non linear relationships
Multiple linear relationships

e.g. Curved so no 'pmcc' can be made

e.g. Shows more than 1 relationship so 'pmcc' would be misleading