Vectors on a Plane (3D Vectors)
Information
A plane is a 2-D body that is used to find vectors perpendicular to certain areas as now we are working in 3-D without this area there would be infinite perpendicular vectors as we have 360° to work with now
For example the grey area below shows the plane that we may need to find perpendicular vectors to
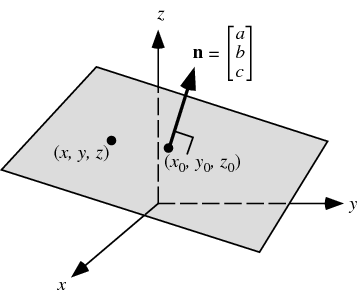
The equation for a plane can be found using the equation below and rplacing the values with the vectors that create the plane
$$\underline{r} = \vec{OA} + λ\vec{AB} + μ\vec{AC}$$
This can be written as:
$$\underline{r} = \underline{a} + λ(\underline{b}-\underline{a}) + μ(\underline{c}-\underline{a})$$
Inputting the values for the vectors and solving allows us to get this in the general equation:
$$ax+by+cz+d=0$$
Find the equation of the plane through A(4,2,0),B(3,1,1) and C(4,-1,1)
Using the equation:
$$\underline{r} = \vec{OA} + λ\vec{AB} + μ\vec{AC}$$
$$\underline{r} = \begin{pmatrix}4\\\ 2\\\ 0\end{pmatrix} + λ\begin{pmatrix}-1\\\ -1\\\ 1\end{pmatrix} + μ\begin{pmatrix}0\\\ -3\\\ 1\end{pmatrix}$$
Now we need to find the x,y and z values for this plane
Solving for x (Equation 1):
x = 4-λ+0μ = 4-λ
λ = 4-x
Solving for y (Equation 2):
y = 2-λ-3μ
Solving for z (Equation 3):
z = 0+λ+μ = λ+μ
Using Equation 1 to replace λ in Equation 2 and 3 we get:
y = 2-(4-x)-3μ = -2+x-3μ
z = (4-x)+μ
Now we need to find a way to remove the μ value which can be done by making the equations have the same μ value and either adding or subtracting them to remove it
To do this we can multiply the z equation by 3 so we have the Equation:
3z = 3(4-x+μ) = 12-3x+3μ
Now we can add these two equations together and we get:
3z+y = 12-3x+3μ-2+x-3μ
3z+y = 10-2x
Rearranging this equation gives us:
2x+y+3z-10 = 0
This is now in the general equation frormat that we discussed earlier:
$$ax+by+cz+d=0$$
Question 1
Find the equation of the plane in vector and cartesian form
The normal (perpendicular) to a plane is
$$\begin{pmatrix}1\\\ -5\\\ 8\end{pmatrix}$$
and passes through
$$\begin{pmatrix}3\\\ 2\\\ 7\end{pmatrix}$$
We know from the previous lesson that when two vectors are perpendicular there scalar product is equal to 0 as:
cos90° = 0
This means that the vector r is perpendicualar to the plane (1,-5,8) and we can therefore set their scalar products equal to eachother like so knowing that any remainder will be the value for d (distance) as we already have the values for x,y and z:
(x=1, y=-5 and z=8)
$$r·\begin{pmatrix}1\\\ -5\\\ 8\end{pmatrix}$$
=
$$\begin{pmatrix}3\\\ 2\\\ 7\end{pmatrix}·\begin{pmatrix}1\\\ -5\\\ 8\end{pmatrix}$$
(Vector form of the eqaution is shown below)
$$r·\begin{pmatrix}1\\\ -5\\\ 8\end{pmatrix}$$
=
$$(3×1)+(2×[-5])+(7×8)=49$$
Therefore this means that the distanve of the vector d = 49
To complete the equation we need to write down the value of the whole equation in cartesian form
$$\begin{pmatrix}x\\\ y\\\ z\end{pmatrix}·\begin{pmatrix}1\\\ -5\\\ 8\end{pmatrix}$$
=
$$x-5y+8z=49$$
x - 5y + 8z - 49 = 0
Question 2
Write the equation of the plane through (2,1,3), given that the vector (4,5,6) is perpendicular
$$r·\begin{pmatrix}4\\\ 5\\\ 6\end{pmatrix}$$
=
$$\begin{pmatrix}2\\\ 1\\\ 3\end{pmatrix}·\begin{pmatrix}4\\\ 5\\\ 6\end{pmatrix}$$
$$r·\begin{pmatrix}4\\\ 5\\\ 6\end{pmatrix}$$
=
$$(2×4)+(1×5)+(3×6)=31$$
Therefore the distance of the vector is d = 31
$$\begin{pmatrix}x\\\ y\\\ z\end{pmatrix}·\begin{pmatrix}4\\\ 5\\\ 6\end{pmatrix}$$
=
$$4x+5y+6z=31$$
4x + 5y + 6z - 31 = 0
Intersection of a line and a plane
Find the point of intersection between the line
The normal (perpendicular) to a plane is
$$r=\begin{pmatrix}2\\\ 3\\\ 4\end{pmatrix}+λ\begin{pmatrix}1\\\ 2\\\ -1\end{pmatrix}$$
with plane
$$5x+y-z=1$$
First we need to replace r with the matrix (x,y,z) in order to find the values of x,y and z
$$\begin{pmatrix}x\\\ y\\\ z\end{pmatrix}$$
=
$$\begin{pmatrix}2\\\ 3\\\ 4\end{pmatrix}+λ\begin{pmatrix}1\\\ 2\\\ -1\end{pmatrix}$$
We can change this equation into 3 different equations by seperating the matrices into:
x = 2 + λ
y = 3 + 2λ
z = 4 - λ
And we know that 5x+y-z=1
Replacing the values of x,y and z with these new values we get the new equation:
5(2+λ) + (3+2λ) - (4-λ) = 1
10+5λ + 3+2λ - 4+λ = 1
8λ = -8
λ = -1
$$\begin{pmatrix}x\\\ y\\\ z\end{pmatrix}$$
=
$$\begin{pmatrix}2\\\ 3\\\ 4\end{pmatrix}+(-1)\begin{pmatrix}1\\\ 2\\\ -1\end{pmatrix}$$
x = 2-1 = 1
y = 3-2 = 1
z = 4+1 = 5
Point of intersection = (1,1,5)
Distance of a Point from a Plane
A is the point (7,5,3) and plane π has the equation 3x+2y+z=6
Find the equation of the line through A perpendicular to the plane π
$$r = \begin{pmatrix}7\\\ 5\\\ 3\end{pmatrix}+λ\begin{pmatrix}3\\\ 2\\\ 1\end{pmatrix}$$
Find the point (P) of intersection with the line r and the plane π
$$\begin{pmatrix}x\\\ y\\\ z\end{pmatrix} = \begin{pmatrix}7\\\ 5\\\ 3\end{pmatrix}+λ\begin{pmatrix}3\\\ 2\\\ 1\end{pmatrix}$$
x = 7 + 3λ
y = 5 + 2λ
z = 3 + λ
Using the equation of the plane
3x+2y+z=6 we get:
3(7+3λ) + 2(5+2λ) + (3+λ) = 6
21 + 9λ + 10 + 4λ + 3 + λ = 6
14λ = -28
λ = -2
$$P = \begin{pmatrix}7\\\ 5\\\ 3\end{pmatrix}-2\begin{pmatrix}3\\\ 2\\\ 1\end{pmatrix}$$
$$P = \begin{pmatrix}7\\\ 5\\\ 3\end{pmatrix}-\begin{pmatrix}6\\\ 4\\\ 2\end{pmatrix} = \begin{pmatrix}1\\\ 1\\\ 1\end{pmatrix}$$
$$P = (1,1,1)$$
Find the distance
$$\vec{|AP|}$$
$$\vec{AP} = P-A = \begin{pmatrix}1\\\ 1\\\ 1\end{pmatrix}-\begin{pmatrix}7\\\ 5\\\ 3\end{pmatrix} = \begin{pmatrix}-6\\\ -4\\\ -2\end{pmatrix}$$
$$\vec{|AP|} = \sqrt{6^2+4^2+2^2} = \sqrt{56}$$
Finding angles between 3D Vectors
Find the angle between the vectors p and q in degrees to 1dp where:
$$\underline{p} = 3\underline{i}-2\underline{j}+7\underline{k}$$
$$\underline{q} = \underline{i}+6\underline{j}-4\underline{k}$$
Using knowledge from earlier in Unit 1 we know the equation to find the angle of a vector is:
$$cosθ = \frac{a·b}{|ab|}$$
$$a·b = (3×1)+([-2]×6)+(7×[-4]) = -37$$
$$|ab| = |a|×|b| = \sqrt{3^2+2^2+7^2}×\sqrt{1^2+6^2+4^2} = \sqrt{62}×\sqrt{53}$$
Inputting this into our equation we get:
$$cosθ = \frac{-37}{\sqrt{62}×\sqrt{53}}$$
Rearranging this becomes:
$$θ = cos^{-1}(\frac{-37}{\sqrt{62}×\sqrt{53}}) = 130.2°$$
Position vectors A and B are represented by the vectors a and b. Points C and D have position vectors 4a-b and -10a+5b
Point E lies on the line CD such that the ratio:
CE:ED=1:3
First we should represent this information in a sketch diagram as we do not know the values of A and B but we do know that the Origin (O),C and D form a triangle and that on the line CD lies E in a 1:3 ratio between the two
Using this information we can sketch the graph below to help visualise the vectors
(Remember the ratio 1:3 leaves the fractions 1/4 and 3/4 as there are 4 parts the the ratio[1+3])
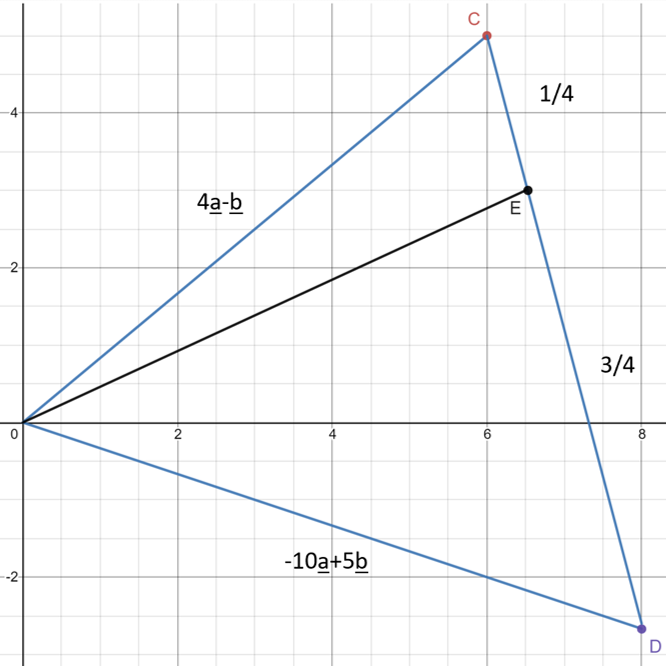
Find the expression for the position vector of point E in terms of a and b
$$\vec{|OE|} = \vec{|OC|} + \frac{1}{4}\vec{|CD|}$$
We can do this as on the graph we can see that by tracing the line OC and 1/4 of CD we will land at point E
Filling in the values we know we will find that:
$$\vec{|CD|} = D-C = (-10\underline{a}+5\underline{b})-(4\underline{a}-\underline{b}) = -14\underline{a}+6\underline{b}$$
$$\vec{|OE|} = 4\underline{a}-\underline{b} + \frac{1}{4}(-14\underline{a}+6\underline{b}) = 4\underline{a}-\underline{b} - \frac{7}{2}\underline{a}+\frac{3}{2}\underline{b})$$
$$\vec{|OE|} = \frac{1}{2}\underline{a}+\frac{1}{2}\underline{b}$$
This means that point E lies at:
$$E = \frac{1}{2}\underline{a}+\frac{1}{2}\underline{b}$$