Vectors
Information
We have already been exploting vectors without you maybe have realising it in the complex numbers topics
This means we can build from the knowledge that you already know from those topics
I would recommend revisiting those sections if you would like to remind yourself of the equations as we will be using those equations already discussed to switch between Cartesian and Polar Form as well as finding magnitudes
We will start with some easier questions to remind you of the knowledge you have previously gained
Question 1
Write (5,60°) in component form (Cartesian Form)
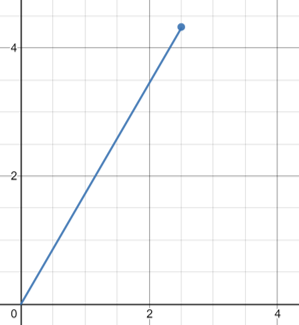
This means we know the radius(r)=5 and the angle is 60° so we can use this in the equations previously learned to find the values of y and x
$$sin(60°)= \frac{y}{5}$$
$$cos(60°)= \frac{x}{5}$$
Rearranging these equations gives us:
y = 5sin(60°) = 4.33
x = 5cos(60°) = 2.5
As the point is in the top right box and we have 2 positive values we do not need to alter them in any way therefore the answer is:
$$2.5\underline{i} + 4.33\underline{j}$$
Note that vectors are written with an underline or a bold such as i j
Question 2
Write (10,290°) in component form (Cartesian Form)
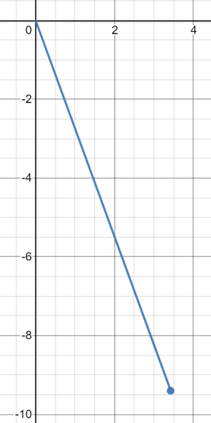
$$sin(290°)= \frac{y}{10}$$
$$cos(290°)= \frac{x}{10}$$
Rearranging these equations gives us:
y = 10sin(290°) = 9.40
x = 10cos(290°) = 3.42
As the point is in the bottom right box and we have 2 positive values, therefore we need to alter the y value as we currently have a positive value when we are expecting a negative one:
$$3.42\underline{i} - 9.40\underline{j}$$
Question 3
Write
$$-5\underline{i} + 4\underline{j}$$
in Polar form or Magnitude direction form
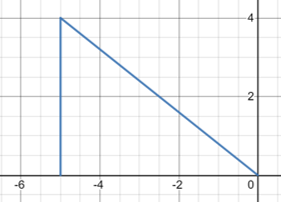
$$|a|=\sqrt{4^2+5^2} = \sqrt{41} = 6.4$$
$$θ = tan^{-1}(\frac{4}{5}) = 39°$$
(6.4,39°)
Question 4
Points L,M and N have co-ordinates (4,3), (-2,-1) and (2,2)
Find the position vector of
$$\vec{L}$$
and vector
$$\vec{MN}$$
$$\vec{L} = 4\underline{i} + 3\underline{j}$$
$$\vec{MN} = \vec{N} - \vec{M} = (2\underline{i} + 2\underline{j}) - (-2\underline{i} - 1\underline{j}) = 4\underline{i} + 3\underline{j}$$
What does this answer tell you about the lines
$$\vec{OL}$$
and
$$\vec{MN}$$
This means that the two lines are the same lenth as:
(O is the origin)
$$\vec{OL} = \vec{L} - \vec{O} = (4\underline{i} + 3\underline{j}) - (0\underline{i} + 0\underline{j}) = 4\underline{i} + 3\underline{j}$$
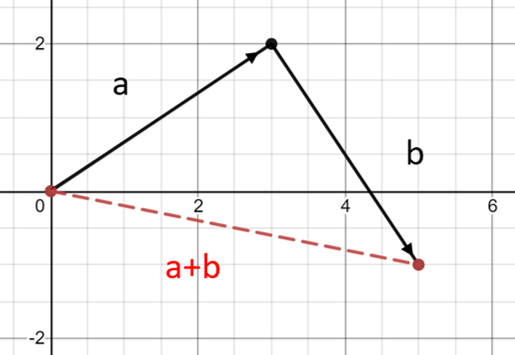
Adding Vectors
If vector
$$\vec{a} = (3\underline{i} + 2\underline{j})$$
then vector
$$\vec{-a}= -(3\underline{i} + 2\underline{j}) = -3\underline{i} - 2\underline{j}$$
If we have vector
$$\vec{a} = 3\underline{i} + 2\underline{j}$$
and vector
$$\vec{b}= 2\underline{i} - 3\underline{j}$$
What is
$$\vec{a}+\vec{b}$$
$$\vec{a}+\vec{b} = (3\underline{i} + 2\underline{j}) + (2\underline{i} - 3\underline{j}) = 5\underline{i} - \underline{j}$$
Question 5
If P has Co-ordinates (2,1) and Q has Co-ordinates (3,5)
Find the vectors:
$$\vec{PQ}$$
and
$$\vec{QP}$$
We know these will give different answers as what we are calculating is the distance that the second point is from the first point so we will have answers with opposite signs as the distance will remain the same between the two points but the direction we are travelling will change
(If we think of the first point as the origin we are calculating where the new point is in respect to that new origin)
$$\vec{PQ} = (3\underline{i} + 5\underline{j}) - (2\underline{i} + 1\underline{j}) = \underline{i} + 4\underline{j}$$
$$\vec{QP} = (2\underline{i} + 1\underline{j}) - (3\underline{i} + 5\underline{j}) = -\underline{i} - 4\underline{j}$$
Unit Vectors
The unit vector of the vector
$$\vec{a}$$
is written as
$$\hat{a}$$
If the vector
$$\vec{a} = 3\underline{i} + 5\underline{j}$$
What is the unit vector?
Magnitude
$$= \sqrt{3^2+5^2} = \sqrt{34}$$
To find the unit vector we simply divide the vector by the magnitude
$$\hat{a} = \frac{3}{\sqrt{34}}\underline{i} + \frac{5}{\sqrt{34}}\underline{i}$$
Vector Equation of a Line
The vector equation of a line allows us to easily find points that are in the same line as the line between two vector points
We can follow this line between the two points to find the midpoint or to find any point on the line and even past the points the line was formed from
Given Points A(2,-1), B(4,3) draw the line AB
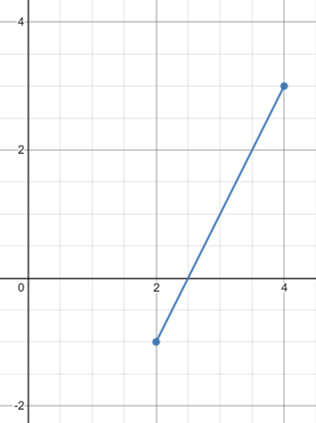
All we need to do is draw the line AB we can do this by either plotting the two points and drawing a line between them
or we can plot A and find the line AB by:
$$\vec{AB} = (4\underline{i} + 3\underline{j}) - (2\underline{i} - 1\underline{j}) = 2\underline{i} + 4\underline{j}$$
Find the midpoint of the line
Where M representes the midpoint of the line we can say that:
$$\vec{OM} = \vec{OA} + \frac{\vec{AB}}{2}$$
$$\vec{OM} = (2\underline{i} - \underline{j}) + \frac{2\underline{i} + 4\underline{j}}{2} = 3\underline{i} + \underline{j}$$
Find the point 3/4 of the line from point A to B
Where N representes the point 3/4 of the line from point A to B we can say that:
$$\vec{ON} = \vec{OA} + \frac{3\vec{AB}}{4}$$
$$\vec{ON} = (2\underline{i} - \underline{j}) + \frac{3(2\underline{i} + 4\underline{j})}{4} = (2\underline{i} - \underline{j}) + \frac{(6\underline{i} + 12\underline{j})}{4} = \frac{7}{2}\underline{i} + 2\underline{j}$$
These points can also be found easily by using the vector equation of a line
To create the vector equation of a line all we need is the starting point of the line and the vector of the line
We can then create an equation like below using point A and the vector line AB
Vector Equation of the line AB
$$\vec{OR} = \vec{A} + λ\vec{AB}$$
(Point R = First co-ordinate + [Ratio from first to second point][Direction])
$$\vec{OR} = (2\underline{i} - \underline{j}) + λ(2\underline{i} + 4\underline{j})$$
Now using this equation and replacing lambda(λ) with the amount we are travelling up the line we can easily find the values of OM and ON again
$$\vec{OM} = (2\underline{i} - \underline{j}) + \frac{1}{2}(2\underline{i} + 4\underline{j}) = (3\underline{i} + \underline{j})$$
$$\vec{ON} = (2\underline{i} - \underline{j}) + \frac{3}{4}(2\underline{i} + 4\underline{j}) = (\frac{7}{2}\underline{i} + 2\underline{j})$$
We can even use this equation to find the value of OB by setting lambda(λ) to 1
$$\vec{OB} = (2\underline{i} - \underline{j}) + (1)(2\underline{i} + 4\underline{j}) = (4\underline{i} + 3\underline{j})$$
Finally if we set lambda(λ) to a value that is not between 0 and 1 we can find values that are on the line but are not between points A and B
For example if we wanted to find the point P -3/4 of the distance from A to B:
$$\vec{OP} = (2\underline{i} - \underline{j}) + (-\frac{3}{4})(2\underline{i} + 4\underline{j}) = (2\underline{i} - \underline{j}) + \frac{1}{4}(-6\underline{i} - 12\underline{j}) =(\frac{1}{2}\underline{i} - 4\underline{j})$$
The Point
$$\vec{OA}$$
can also be written as
$$\underline{a}$$
This is the same for all other points meaning that our equation can be more commonly written as:
$$\underline{r} = \underline{a} + λ(\underline{b}-\underline{a})$$
Ways that we see vectors
We can see vectors in multiple different ways for instance we have been using i and j to show where they lie on a graph giving you both there x and y value
However we can also display vectors within a matrix using the top row for the x value and the second row for the y value like so:
$$\underline{a} = 3\underline{i} + 2\underline{j} = \begin{pmatrix}3\\\ 2\end{pmatrix}$$
Sometimes using these matrices can make it easier to add and minus different vectors however it is up to personal preference
We will be using matrices from now on as it is easier to see the calculations being done
However if you wish to carry on using there i and j values there is no issue with this but we would recommend using matrices as they are more commonly used
Changing Forms
First we will look at how to change from vector to cartesian form when we are showing the equation of a line
Given the equation:
$$\underline{r} = \begin{pmatrix}2\\\ -1\end{pmatrix} + λ\begin{pmatrix}1\\\ 2\end{pmatrix} = \begin{pmatrix}x\\\ y\end{pmatrix}$$
x = 2+λ
λ = x-2
y=-1+2λ
2λ=y+1
λ=(y+1)/2
Setting these two equations equal to eachother gives us
x-2=(y+1)/2
2x-4=y+1
y=2x-5
This is our equation of the line and we have therefore now converted from vector form into cartesian form but what about if we wanted to do it the other way around?
Converting cartesian from to vector form
$$y = \frac{x}{3} + 2$$
We want this in the form
$$\underline{r} = $$
1st point + direction
Using the cartesian equation we can find the direction as we know that the gradient of a line is:
$$m = \frac{\text{Change in y}}{\text{Change in x}}$$
We can see that for every time y is increased by 1 x is increases by 1/3 as x is divided by 3 giving us:
$$m = \frac{1}{(\frac{1}{3})}=\frac{3}{1}$$
This means we can write the direction as:
$$\underline{r} = $$
1st point +
$$λ\begin{pmatrix}3\\\ 1\end{pmatrix}$$
Now we juust need to find the 1st point to do this we simply set the value of λ=0 as this is where the line starts
From the equation
$$y = \frac{x}{3} + 2$$
We can see that when x=0 y=2 so this is where our line starts
Therefore the vector equation can be written as:
$$\underline{r} = \begin{pmatrix}0\\\ 2\end{pmatrix} + λ\begin{pmatrix}3\\\ 1\end{pmatrix}$$
Intersection of two lines
What about if we need to find the exact point that two lines intersect knowing only the vector equations of these two lines?
$$\underline{r_1} = \begin{pmatrix}2\\\ 3\end{pmatrix} + λ\begin{pmatrix}1\\\ 2\end{pmatrix}$$
$$\underline{r_2} = \begin{pmatrix}6\\\ 1\end{pmatrix} + μ\begin{pmatrix}1\\\ -3\end{pmatrix}$$
For the two lines to intercept there must be a point when the value of the two equations are the same this means we can set them equal to eachother to find at what point this is true
Equating the y values gives us (Equation 1):
3+2λ=1-3μ
Equating the x values gives us (Equation 2):
2+λ=6+μ
4+2λ=12+2μ
Equation 1 - Equation 2
-1=-11-5μ
10=-5μ
μ=-2
Now we can find the position vector of the intersection point by replacing μ=-2 in the original equation as we know this is when the two lines meet
$$\underline{r_2} = \begin{pmatrix}6\\\ 1\end{pmatrix} - 2\begin{pmatrix}1\\\ -3\end{pmatrix} = \begin{pmatrix}4\\\ 7\end{pmatrix}= 4\underline{i}+7\underline{j}$$
Find the co-ordinates of the point of intersection joining lines:
A(1,6) to B(4,0)
and C(1,1) to D(5,3)
First we need to find the lines that are A to B (r1) and C to D (r2)
Using our previous knowledge we know that the vector equation of a line is made from the 1st point (A and C)
and the direction (B-A and D-C)
$$\underline{r_1} = \begin{pmatrix}1\\\ 6\end{pmatrix} + λ\begin{pmatrix}3\\\ -6\end{pmatrix}$$
$$\underline{r_2} = \begin{pmatrix}1\\\ 1\end{pmatrix} + μ\begin{pmatrix}4\\\ 2\end{pmatrix}$$
We can cancel down the direction of these vectors if they have a common factor as they will have the same value only the value of λ and μ will be different as they will need to be larger to compensate for the factorisation
$$\underline{r_1} = \begin{pmatrix}1\\\ 6\end{pmatrix} + λ\begin{pmatrix}1\\\ -2\end{pmatrix}$$
$$\underline{r_2} = \begin{pmatrix}1\\\ 1\end{pmatrix} + μ\begin{pmatrix}2\\\ 1\end{pmatrix}$$
Now we can repeat what we did for the last quation setting the x and y values equal to eachother as this will be the intersection point
Equating the y values gives us (Equation 1):
6-2λ=1+μ
Equating the x values gives us (Equation 2):
1+λ=1+2μ
2+2λ=2+4μ
Equation 1 + Equation 2
8=3+5μ
5=5μ
μ=1
Now we can find the position vector of the intersection point by replacing μ=-2 in the original equation as we know this is when the two lines meet
$$\underline{r_2} = \begin{pmatrix}1\\\ 1\end{pmatrix} + 1\begin{pmatrix}2\\\ 1\end{pmatrix} = \begin{pmatrix}3\\\ 2\end{pmatrix}= 3\underline{i}+2\underline{j}$$
Angles between two vectors
The angle between two vectors can be found using this equation:
$$cosθ = \frac{\underline{a} · \underline{b}}{|a||b|}=\frac{\text{Scalar Product}}{\text{Multiply Vector Magnitudes}}$$
Scalar Product:
Scalar Product of
$$\begin{pmatrix}4\\\ 3\end{pmatrix} \text{ and } \begin{pmatrix}3\\\ 2\end{pmatrix} = (x_1×x_2)+(y_1×y_2) = (4×3)+(3×2) = 24+6 = 30$$
What happens when the angle on the two vecors is 90°?
Using the Equation to find the angle we can see
$$cos90° = \frac{\underline{a} · \underline{b}}{|a||b|}=\frac{\text{Scalar Product}}{\text{Multiply Vector Magnitudes}}$$
However we know that cos90°=0 this means that the entire equation is equal to 0:
$$0 = \frac{\underline{a} · \underline{b}}{|a||b|}=\frac{\text{Scalar Product}}{\text{Multiply Vector Magnitudes}}$$
The only way this can be true is if the scalar product also equals 0
This means we can find out easily if two vectors are perpendicular as there scalar product will equal 0
We can also use this knowledge to find the perpendicular vectors as well as we know the scalar product must equal 0
Vector Magnitudes:
Vector Magnitudes of
$$\begin{pmatrix}4\\\ 3\end{pmatrix} \text{ and } \begin{pmatrix}3\\\ 2\end{pmatrix} = \sqrt{x_1^2+y_1^2}×\sqrt{x_2^2+y_2^2} = \sqrt{4^2+3^2}×\sqrt{6^2+2^2} = \sqrt{25}×\sqrt{40} = 10\sqrt{10}$$
Therefore the angle between these two vectors is:
$$cosθ = \frac{30}{10\sqrt{10}}=\frac{3}{\sqrt{10}}=0.949$$
$$θ = cos^{-1}(\frac{3}{\sqrt{10}}) = 18.4°$$
Find the angle between vectors a and b where:
$$\underline{a} = \begin{pmatrix}3\\\ 4\end{pmatrix}$$
$$\underline{b} = \begin{pmatrix}5\\\ -12\end{pmatrix}$$
$$\underline{a}·\underline{b} = (3×5)+(4×-12) = 15-48 = -33$$
$$|a||b|=\sqrt{3^2+4^2}×\sqrt{5^2+(-12)^2}=\sqrt{25}×\sqrt{169}=5×13=65$$
Therefore the angle between these two vectors is:
$$cosθ = \frac{-33}{65}=-0.508$$
$$θ = cos^{-1}(frac{-33}{65}) = 120.5°$$
3-D Vectors
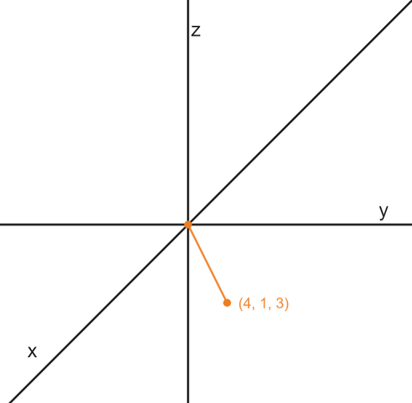
3-D Vectors have an x,y and z position meaning that we need three axis on which to plot them
This means we introduce the k value to the i and j in order to represent the z-axis like so:
(Where x=4, y=1 and z=3)
$$4\underline{i} + \underline{j} + 3\underline{k}= \begin{pmatrix}4\\\ 1 \\\ 3\end{pmatrix} $$
To find the magnitude of a 3-D Vector we just have 3 values under the root instead of 2 like so:
$$|a|=\sqrt{x^2+y^2+z^2}=\sqrt{4^2+1^2+3^2}=\sqrt{26}$$
Find the angle between the vectors a and b where:
$$\underline{a} = \begin{pmatrix}3\\\ 4 \\\ 1\end{pmatrix}$$
$$\underline{b} = \begin{pmatrix}5\\\ -2 \\\ 3\end{pmatrix}$$
$$\underline{a}·\underline{b} = (x_1×x_2)+(y_1×y_2)+(z_1×z_2) = (3×5)+(4×-2)+(1×3) = 15-8+3 = 10$$
$$|a||b|=\sqrt{3^2+4^2+1^2}×\sqrt{5^2+(-2)^2+3^2}=\sqrt{26}×\sqrt{36}=6\sqrt{26}$$
Therefore the angle between these two vectors is:
$$cosθ = \frac{10}{6\sqrt{26}}$$
$$θ = cos^{-1}(\frac{10}{6\sqrt{26}}) = 71.44°$$
3-D Vector Equation of a line
$$\underline{r} = \begin{pmatrix}3\\\ 4\\\ 1\end{pmatrix} + λ\begin{pmatrix}2\\\ 1\\\ -1\end{pmatrix}$$
has position
$$\begin{pmatrix}3\\\ 4\\\ 1\end{pmatrix}$$
and direction
$$\begin{pmatrix}2\\\ 1\\\ -1\end{pmatrix}$$
Find the equation of the line
In order to find the equation of the line we need to find the values of x,y and z in terms of λ and then we can set them equal to eachother
To do this we do the same as we did with 2-D vectors and take the x,y and z terms from the equation seperately like so:
First we find the equation for x:
$$x=3+2λ$$
$$x-3=2λ$$
$$λ=\frac{x-3}{2}$$
Now we find the equation for y:
$$y=4+λ$$
$$λ=\frac{y-4}{1}$$
Finally we find the equation for z:
$$z=1-λ$$
$$λ=\frac{z-1}{-1}$$
Setting all these equations as equal to eachother gives us the vector equation of the line:
$$\frac{x-3}{2}=\frac{y-4}{1}=\frac{z-1}{-1}$$
This can be re-written as:
$$\frac{x-3}{2}=y-4=-z+1$$