Polynomials Contd.
Information
(α+β)²
(α+β)² = α² + 2αβ + β²
Therefore:
α² + β² = (α+β)² - 2αβ
(α+β)³
(α+β)³ = (α+β)²(α+β)
(α+β)³ = (α² + 2αβ + β²)(α+β)
(α+β)³ = α³ + 2α²β + αβ² + α²β + 2αβ² + β³
(α+β)³ = α³ + 3α²β + 3αβ² + β³
Therefore:
α³ + β³ = (α+β)³ - 3α²β - 3αβ²
α³ + β³ = (α+β)³ - 3αβ(α+β)
(α+β+γ)²
(α+β+γ)² = α² + 2αβ + 2αγ + β² + 2βγ + γ²
(α+β+γ)² = α² + β² + γ² + 2(αβ+αγ+βγ)
Therefore:
α² + β² + γ² = (α+β+γ)² - 2(αβ+αγ+βγ)
k(x-α)(x-β)
ax² + bx + c = k(x-α)(x-β)
ax² + bx + c = k(x² - αx - βx + αβ)
We can now equate the x²,x and constant values to find the values of a,b and c
ax² = kx²
Therefore:
a = k
bx = k(-αx - βx) = -k(αx + βx)
Therefore:
b = -k(α + β)
c = k(αβ)
As we know a = k we can replace k in all of these equations such that:
| -b |
| a |
= α + β
| c |
| a |
= αβ
k(x-α)(x-β)(x-γ)
ax³ + bx² + cx + d = k(x-α)(x-β)(x-γ)
ax³ + bx² + cx + d = k(x² - αx - βx + αβ)(x-γ)
ax³ + bx² + cx + d = k(x³ -αx² - βx² - γx² + αβx + αγx + βγx - αβγ)
We can now equate the x²,x and constant values to find the values of a,b and c
ax³ = kx³
Therefore:
a = k
bx² = k(-αx² - βx² - γx²) = -k(αx + βx + γx²)
Therefore:
b = -k(α + β + γ)
cx = k(αβx + αγx + βγx)
c = k(αβ + αγ + βγ)
d = k(-αβγ) = -k(αβγ)
As we know a = k we can replace k in all of these equations such that:
| -b |
| a |
= α + β + γ
| c |
| a |
= αβ + αγ + βγ
| -d |
| a |
= αβγ
From this we can see a pattern where as we increase the power on the x and hence the amount of (x-constant) brackets we get:
(e.g.For x to the power of 4)
a is always equal to k and positive
Next the sign flips so b is negative and when divided by a is the sum of all the constants
-b/a = sum of all constants
(e.g. α + β + γ + δ)
Then the sign flips again so c is positive and when divided by a is the sum of all pairs of constants
c/a = sum of all pairs of constants multiplied
(e.g. αβ + αγ + αδ + βγ + βδ + γδ)
Then the sign flips again so d is negative and when divided by a is the sum of all trios of constants
-d/a = sum of all trios of constants multiplied
(e.g. αβγ + αβδ + αγδ + βγδ)
Finally the sign flips again so e is positive and when divided by a is all four constants multiplied
(e.g. αβγδ)
Example
3x² - 7x + 11
-b/a = α + β = -(-7/3) = 7/3
c/a = αβ = 11/3
Question 1
Find a quadratic equation whose roots have sum 1/2 and product of -5/2
α + β = -b/a = 1/2
αβ = c/a = -5/2
We can therefore see that:
a = 2
b = -1
c = -5
Therefore the equation of the quadratic whose roots have sum 1/2 and product of -5/2 is:
2x² - x - 5 = 0
Question 2
Equation 4x² + 7x - 5 = 0 has roots α and β find equation with roots α² and β²
-b/a = α + β = -(7/4)
c/a = αβ = -5/4
Using the equation shown above we know that:
(α+β)² = α² + 2αβ + β²
Therfore to find the sum of the new roots α² and β² we can rearrange such that:
-b/a = α² + β² = (α+β)² - 2αβ
Filling in our values for α and β we get:
α² + β² = (-7/4)² - 2(-5/4)
α² + β² = 49/16 + 10/4 = 89/16
-b/a = 89/16
Now to find the product α²β² = (αβ)²:
c/a = (-5/4)² = 25/16
From these values we now know that:
a = 16
b = -89
c = 25
This gives us the quadratic equation:
16x² - 89x +25 = 0
Question 3
Find equation with the roots 4,3 and -2
We can use these values to represent α,β and γ in our equations:
(α = 4,β = 3,γ = -2
-b/a = α + β + γ
-b/a = 4 + 3 + (-2) = 5
c/a = αβ + αγ + βγ
c/a = (4)(3) + (4)(-2) + (3)(-2) = 12 - 8 - 6 = -2
-d/a = αβγ
-d/a = (4)(3)(-2) = -24
Using these values we know that:
a = 1
b = -5
c = -2
d= 24
This makes the cubic equation:
x³ - 5x² - 2x + 24 = 0
Question 4
x³ + 3x² - 7x + 2 = 0 has roots α,β and γ find the value of α² + β² + γ²
α + β + γ = -b/a = -3/1
αβ + αγ + βγ = c/a = -7/1
αβγ = -d/a = -2/1
We know that:
α² + β² + γ² = (α+β+γ)² - 2(αβ+αγ+βγ)
From previous work, using this equation and filling in the values we get:
α² + β² + γ² = (-3)² - 2(-7) = 23
Question 5
x4 - 3x³ + 12x² + 126x - 136 = 0 has roots α,β,γ and δ
Part a
Prove α² + β² + γ² + δ² = -15
(α + β + γ + δ)² = α² + β² + γ² + δ² + 2(αβ + αγ + αδ + βγ + βδ + γδ)
α + β + γ + δ = -b/a = -(-3)/1 = 3
αβ + αγ + αδ + βγ + βδ + γδ = c/a = 12/1 = 12
As these are tthe only values in the equation we dont need do any more equations
(α + β + γ + δ)² = α² + β² + γ² + δ² + 2(αβ + αγ + αδ + βγ + βδ + γδ)
α² + β² + γ² + δ² = (α + β + γ + δ)² - 2(αβ + αγ + αδ + βγ + βδ + γδ)
α² + β² + γ² + δ² = (3)² - 2(12) = -15
Part b
Deduce how many roots x4 - 3x³ + 12x² + 126x - 136 = 0 has
We know that this polynomial must have 4 roots as the highest power of x is 4 and there are always as many toots as the highest power
(e.g.x4 = 4 roots)
We now need to figure out hpw many real and imaginary roots there are
We know imaginary roots come in pairs so there are either:
4 real roots
2 real, 2 imaginary roots
4 imaginary roots
To find out how many of each roots there are we can either use a calculator to tell us or we can sketch a graph like the one below and count how many times the polynomial crosses the x axis
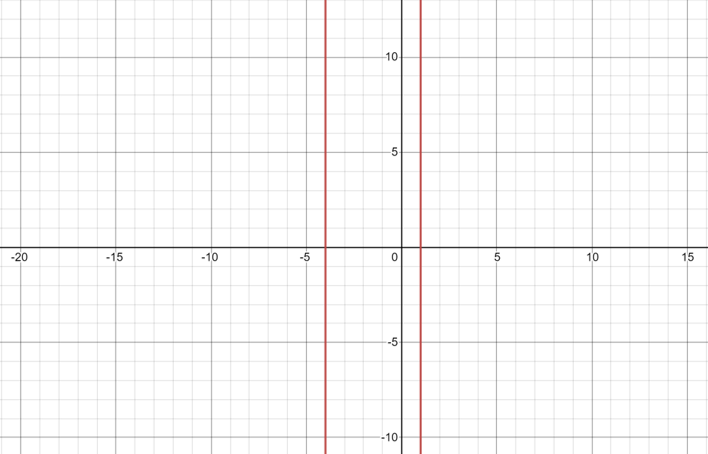
As we can see in this graph there are 2 crossing pints this means we have:
2 real and 2 imaginary roots
This can be just as easily achieved putting these values into a calculator
Part c
Find the equations whose roots are 2α+3, 2β+3, 2γ+3 and 2δ+3
We know from part a that the equation:
x4 - 3x³ + 12x² + 126x - 136 = 0 has roots α,β,γ and δ
We know that for the equation to equal 0 x must be equal to either α,β,γ and δ as then one bracket becomes zero
(e.g. When x = α then (x-α) = 0 meaning the value of the equation becomes 0)
If we now set the value y equal to the new roots we can find the new equation:
y = 2α+3
y = 2β+3
y = 2γ+3
y = 2δ+3
As you can see all these equations are identical so we only need to solve one:
α =
| y - 3 |
| 2 |
We also know that x = α so this means
x =
| y - 3 |
| 2 |
We can now replace x with ths=is new value to find the new equation from:
x4 - 3x³ + 12x² + 126x - 136 = 0
([y-3]/2)4 - 3([y-3]/2)³ + 12([y-3]/2)² + 126([y-3]/2) - 136 = 0
Solving all these brackets using a calculator
(Remember ([y-3]/2)³ means ([y-3]/2)([y-3]/2)([y-3]/2) so we will get extra values for y³,y²,y and the constant as well)
We find that the equation with roots 2α+3, 2β+3, 2γ+3 and 2δ+3 is:
y4 - 18y³ + 156y² + 450y - 4525 = 0
Question 6
Given the equation x³ + 2x² - x + 28 = 0 has an integer root determine all 3 roots
The equation having an integer root means at least one root is real we can use this knowledge to find one of the roots using previous knowledge from the first polynomials lesson:
Fist we find the factors of 28 which are:
±1, ±2, ±4, ±7, ±14, ±28
We then need to replace x with these values until we find our factor:
f(-1)= (-1)³ + 2(-1)² - (-1) + 28 = 30 so 1 is not a factor
f(-2)= (-2)³ + 2(-2)² - (-2) + 28 = 30 so 2 is not a factor
f(-2)= (-4)³ + 2(-4)² - (-4) + 28 = 0 so 4 is a factor
(factor if 4 as when x = -4 the factor is [-4 + 4] = 0 therefore the equation equals 0)
We now need to divide this root from the original equation to see what we are left with:
| x³ + 2x² - x + 28 |
| (x + 4) |
= x² - 2x + 7
This means (x² - 2x + 7)(x + 4) = 0
We can now use the quadratic formula in order to find out the other roots to the equation
\[{-b \pm \sqrt{b^2-4ac} \over 2a}\]
=
\[{-(-2) \pm \sqrt{(-2)^2-4(1)(7)} \over 2(1)}\]
\[{2 \pm \sqrt{-24} \over 2}\]
=
\[{2 \pm \sqrt{4×6×i^2} \over 2}\]
=
\[{2 \pm 2i \sqrt{6} \over 2}\]
1 ± i\(\sqrt{6}\)
This means we have found the other 2 roots to the equation which are:
1 + i\(\sqrt{6}\)
1 - i\(\sqrt{6}\)
Therefore the equation becomes:
(x + 4)(x - [1 + i\(\sqrt{6}\)])(x - [1 - i\(\sqrt{6}\)]) = 0
(x + 4)(x - 1 - i\(\sqrt{6}\))(x - 1 + i\(\sqrt{6}\)) = 0
Question 7
x4 - 2x³ - 2x² + 6x + 5 = 0
Given one root is 2+i find all other roots
We know that complex roots come in pairs with there complex conjugate therefore we know another root must be:
2 - i
Multiplying these two roots together we find that:
(x - 2 - i)(x - 2 + i) = x² - 4x + 4 + 1 = x² - 4x + 5
We can now divide this from the orignial equation like so:
| x4 - 2x³ - 2x² + 6x + 5 |
| x² - 4x + 5 |
= x² + 2x + 1
Solving x² + 2x + 1 using the quadratic formula or a calculator gives us the roots:
(x+1)(x+1) or (x+1)²
This means that the roots are:
(x+1)²(x-2-i)(x-2+i) = 0
x = -1, 2+i , 2-i