Matrices Transformations
Information
Matrices Transformations are used to change the elements of a matrix/matrices so that they are either rotated, enlarged, shrunk, reflected or there posistion moved.
Rotate
When rotating around a graph all points are rotated anticlockwise about the origin so all points start and end the same distance from the origin when rotated
(The origin is at Point 0,0)
Q(0,2), R(1,2), P(0,1), S(1,1)
Q'(-2,0), R'(-2,1), P'(-1,0), S'(-1,1)
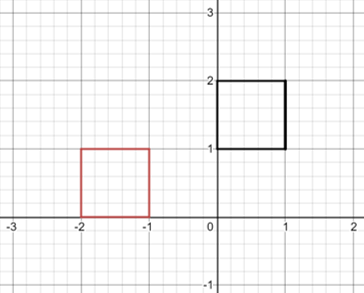
In order to rotate a matrix 90° you must multiply it like followed below:
| -1 | 0 |
| 0 | 1 |
| 2 |
| 3 |
=
| -3 |
| 2 |
| -1 | 0 |
| 0 | 1 |
| x |
| y |
=
| -y |
| x |
Reflected on the y axis
When reflecting on the y axis all points start and end the same distance from the origin however the x value now becomes the opposite sign
(e.g. + to - or - to +) as it has been flipped to the other side of the graph
(The origin is at Point 0,0)
Q(2,0), R(2,1), P(1,0), S(1,1)
Q'(-2,0), R'(-2,1), P'(-1,0), S'(-1,1)
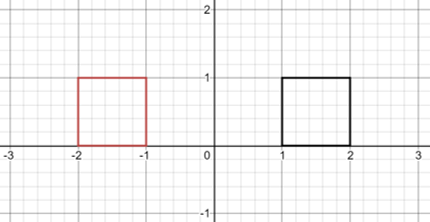
In order to reflect a matrix upon the y axis you must multiply it like followed below:
| 0 | -1 |
| 1 | 0 |
| 1 |
| 2 |
=
| -1 |
| 2 |
| 0 | -1 |
| 1 | 0 |
| x |
| y |
=
| -x |
| y |
Enlarge or shrink by factor f
When reflecting on the y axis all points start and end the same distance from the origin however the x value now becomes the opposite sign
(e.g. + to - or - to +) as it has been flipped to the other side of the graph
(The origin is at Point 0,0)
Q(1,2), R(2,2), P(1,1), S(2,1)
Q'(2,4), R'(4,4), P'(2,2), S'(4,2)
(This image shows a scale factor of 2)
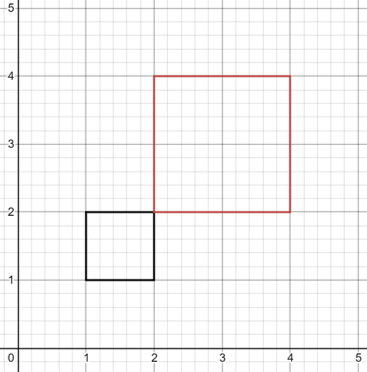
In order to enlarge or shrink a matrix you must multiply it like followed below:
| f | 0 |
| 0 | f |
| -2 |
| 3 |
=
| f X (-2) |
| f X 3 |
| f | 0 |
| 0 | f |
| x |
| y |
=
| f X x |
| f X y |
Below is a matrix example that has a scaling factor of 2:
| 2 | 0 |
| 0 | 2 |
| -1 |
| 3 |
=
| -2 |
| 6 |
Below is a matrix example that has a scaling factor of ½:
| ½ | 0 |
| 0 | ½ |
| 4 |
| -12 |
=
| 2 |
| -6 |
Translation
When Translating we move the position of all the points by the same x and/or y value to itss new spot by introducing a third column for translations
Q(1,2), R(2,2), P(1,1), S(2,1)
Q'(3,4), R'(4,4), P'(3,3), S'(4,3)
(This example shows transaltion of x+2,y+2)
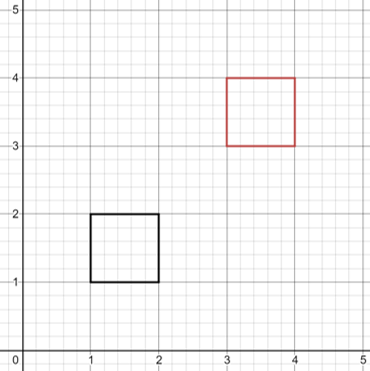
In order to translate a matrix you must multiply it like followed below:
| 1 | 0 | 2 |
| 0 | 1 | 3 |
| 0 | 0 | 1 |
| x |
| y |
| 1 |
=
| x+2 |
| y+3 |
| 1 |
| 1 | 0 | -3 |
| 0 | 1 | 4 |
| 0 | 0 | 1 |
| 4 |
| 2 |
| 1 |
=
| 1 |
| 6 |
| 1 |
| 1 | 0 | a |
| 0 | 1 | b |
| 0 | 0 | 1 |
| x |
| y |
| 1 |
=
| x+a |
| y+b |
| 1 |
Finding Translations from a Question
Points A(1,-1), B(1,3), C(4,3), D(4,1) and E(1,1) are translated so that:
Points above the x axis are moved to the right
Points below the x axis are moved to the left
Points are moved twice the vertical distance they are from the x axis
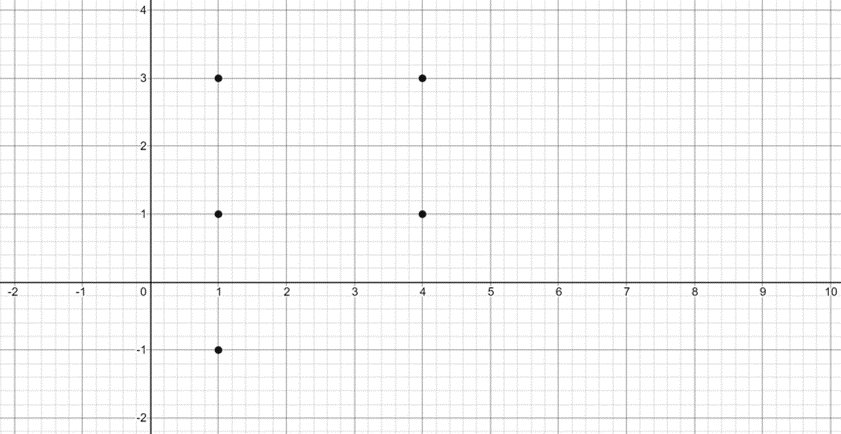
Plot the new locations on the graph so you can see how they have been changed
New locations are A'(-1,-1), B'(7,3), C'(10,3), D'(6,1) E'(3,1)
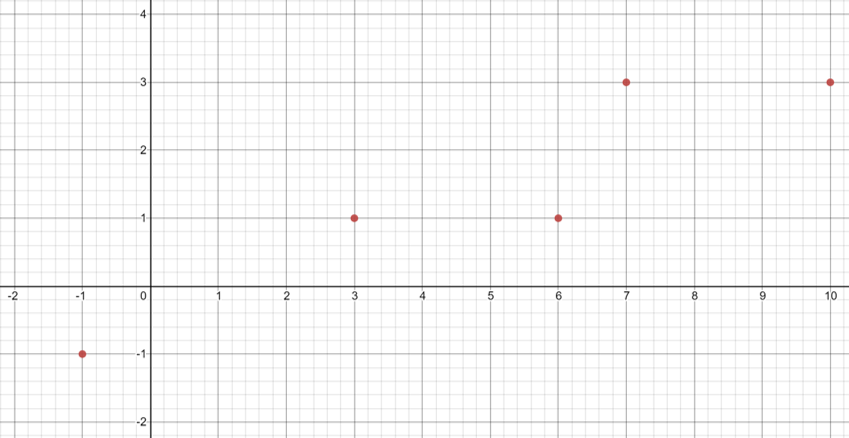
The solution is found by seeing that the new x axis locations are found by:
x' = x+2y and
y' = y
(This means the new value of x is directly effected by the old value of y but y remains the same value)
In matrix form these equations are shown as
| 1 | 2 |
| 0 | 1 |
| x |
| y |
=
| 1 | 2 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| x |
| y |
| 1 |
=
| x+2y |
| y |
| 1 |
Matrices Transformations are used to change the elements of a matrix/matrices so that they are either rotated, enlarged, shrunk, reflected or there posistion moved.
Rotate by θ Degrees
All Points are still rotated anti-clockwise and around the origin however they are now rotated with respect to θ instead of 90°
(The origin is at Point 0,0)
*Important Matrix Below*
| cos0 | -sin0 | 0 |
| sin0 | -cos0 | 0 |
| 0 | 0 | 1 |
As an example in order to rotate by 90° replace all θ's with 90° and you will see we have the same equation as above
| cos(90°) | -sin(90°) | 0 |
| sin(90°) | -cos(90°) | 0 |
| 0 | 0 | 1 |
=
| 0 | -1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
In order to rotate 90° clockwise you instead need to rotate 270° anticlockwise as:
360° - 90° = 270°
| cos(270°) | -sin(270°) | 0 |
| sin(270°) | -cos(270°) | 0 |
| 0 | 0 | 1 |
=
| 0 | 1 | 0 |
| -1 | 0 | 0 |
| 0 | 0 | 1 |
This means as long as you remeber this equation you will be able to rotate by any amount you need to rather than only 90° shown earlier
Multiple Transformation
It is possible to do multiple transformations at the same time on the same Matrix
In order to do this you need to first multiply all the altering matrices together backwards so the last step is the first matrix and the first step is the last matrix to be multiplied
e.g. If you wanted to perform actions A then B then C on a matrix you would multiply them as such
C X B X A X M
(Where M is the Matrix)
Example:
Reflect the Matrix then rotate the matrix 90° clockwise
(Re = Reflect, Ro = Rotate)
(As we are not using translation we can use the 2x2 versions of the matrices)
Re=
| 1 | 0 |
| 0 | -1 |
Ro=
| 0 | -1 |
| 1 | 0 |
Now we multiply thesee in reverse order:
(Re)(Ro)=
| 0 | -1 |
| 1 | 0 |
| 1 | 0 |
| 0 | -1 |
=
| 0 | 1 |
| 1 | 0 |
Finally we use this new matrix and multiply it against the matrix we are Transforming
| 0 | 1 |
| 1 | 0 |
| x |
| y |
=
| y |
| x |
Practice Question
Find h and k where:
Transformation T is the matrix is:
Rotated anti-clockwise about the origin by angle θ (R)
Then T is translated in which point (x,y) transforms to point (x+h,(y+k) (S)
Matrix M(0,1,1) is Transformed into Matrix M'(1,2,1)
Matrix N(3,0,1) is Transformed into Matrix N'(4,3,1)
First find R and S:
R=
| cos(θ) | -sin(θ) | 0 |
| sin(θ) | -cos(θ) | 0 |
| 0 | 0 | 1 |
S=
| 1 | 0 | h |
| 0 | 1 | k |
| 0 | 0 | 1 |
Next Multiply S and R together to find the Translation (T)
T=SR=
| 1 | 0 | h |
| 0 | 1 | k |
| 0 | 0 | 1 |
| cos(θ) | -sin(θ) | 0 |
| sin(θ) | -cos(θ) | 0 |
| 0 | 0 | 1 |
=
| cos(θ) | -sin(θ) | h |
| sin(θ) | -cos(θ) | k |
| 0 | 0 | 1 |
Next multiply by the matrix M(0,1,1) and equal it to M'(1,2,1):
| cos(θ) | -sin(θ) | h |
| sin(θ) | -cos(θ) | k |
| 0 | 0 | 1 |
| 0 |
| 1 |
| 1 |
=
| 1 |
| 2 |
| 1 |
Now multiply by the matrix N(3,0,1) and equal it to N'(4,3,1):
| cos(θ) | -sin(θ) | h |
| sin(θ) | -cos(θ) | k |
| 0 | 0 | 1 |
| 3 |
| 0 |
| 1 |
=
| 4 |
| 3 |
| 1 |
From Multiplying out these 2 equations you find that:
Eqaution 1: -sinθ + h = 1
Eqaution 2: cosθ + k = 2 and
Eqaution 3: 3cosθ + h = 4
Eqaution 4: 3sinθ + k = 3
By adding 3 X Equation 1 to Equation 4 you find:
Equation 5: 3h + k = 6
and by subtracting 3 X Equation 2 from Equation 3 you find:
Equation 6: -h +3k = 2
Finally Adding 3 X Equation 6 to Equation 5 you find:
10k = 12 therefore k = 6/5
Replacing k with 6/5 in equation 6 gives:
-h + 18/5 = 2 meaning h = -2 + 18/5
h = 8/5