Complex Numbers
Information
Polynomials that have a even power such as 2, 4, 6 as the largest power are able to have 0 real roots however those that have odd powers as there largest powers must have at least 1 real root as all complex roots come in conjugate pairs
Adding and Subtracting Complex Numbers
When adding or subtracting complex numbers you can treat the real and imaginary parts of the equations as separate as they do not interact with each other when adding or subtracting
An example of both adding and subtracting Complex numbers will be shown below
Adding:
(3 + 4i) + (-2 + 7i) = x + iy
Seperating the real [R] and imaginary [I] number gives us:
R: 3 - 2 = 1 so the Real part = 1
I: 4i + 7i = 11i so the imaginary part = 11
Therefore x = 1 and y = 11
Subtracting:
(2 + 5i) - (-5 + 2i) = x + iy
Seperating the real [R] and imaginary [I] number gives us:
R: 2 - (-5) = 7 so the Real part = 7
I: 5i - 2i = 3i so the Imaginary part = 3
Therefore x = 7 and y = 3
Multiplying Complex Numbers
When multiplying two complex number you can no longer seperate the terms as they interact with eachother
In order to calculate the answer we must first remember i = √-1
When two Imaginary numbers are multiplied together so are the i's they are with and i² = -1
Rembering this we can now do some examples:
(2i - 5i)(-3 + 4i) = x +iy
-6 + 8i +15i - 20i² = x +iy
-6 + 23i - (20)(-1) = x +iy
-6 + 23i +20 = x +iy
14 + 23i = x +iy
This means x = 14 and y = 23
(8 - 6i)(2 + 7i) = x +iy
16 - 12i + 56i - 42i² = x + iy
16 + 44i + 42 = x + iy
58 + 44i = x + iy
This means x = 58 and y = 44
Dividing Complex Numbers
When dividing two complex number you once again need to remember that i² = -1
Then you can treat the division like you are dividing with surds where you will need to multiply the fraction by the denominator with the complex conjugate of the denominator to cancel out the imaginary part in the denominator
(Remember anything divided by itself is equal to 1 so we can always multiply by a fraction where the denominator and numerator are the same
| (3+2i) |
| (5+i) |
=
| (3+2i) |
| (5+i) |
x
| (5-i) |
| (5-i) |
=
| (3+2i)(5-i) |
| (5+i)(5-i) |
| (3+2i)(5-i) |
| (5+i)(5-i) |
=
| 15+3i+10i-3i² |
| 25+5i-5i-i² |
=
| 18+13i |
| 26 |
Now we have the answer we remember that this fraction = x + iy so we must separate the real and imaginary part of the fraction such that:
This means that the real part = 18/26
The imaginary part = 13/26
Complex Conjugates
We know that the complex conjugate of the complex number z = z* using this information we can add, subtract and multiply the complex conjugates with eachother such as the examples below where:
z = 3 + 5i
w = 1 - 2i
First we need to find the complex conjugates of these numbers where the imaginary part has a sign flip such that:
z* = 3 - 5i
w* = 1 + 2i
Now we have found the complex conjugates we can answer some questions:
Example 1: z + z*
3 + 5i + 3 - 5i = 6
This is used to cancel out the imaginary part of the complex number
Example 2: w - w*
1 - 2i - (1 + 2i) = -4i
This is used to cancel out the real part of the complex number
Example 3: ww*
(1 - 2i)(1 + 2i) = 1 - 2i + 2i - 4² = 5
Example 4: zz*
(3 + 5i)(3 - 5i) = 9 - 15i + 15i - 25i² = 34
Argand Diagrams
A complex number can be represented on something called an argand diagram.
An argand diagram is a graph where instead of x and y being used we instead use real and imaginary parts to plot the point where:
x = real
y = imaginary
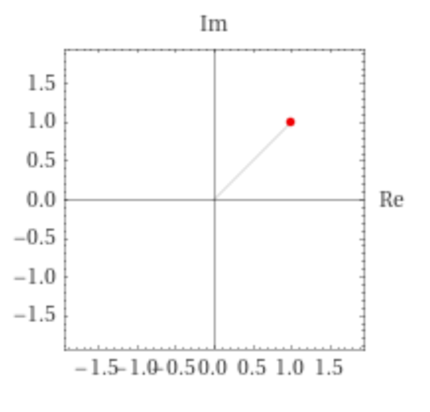
The diagram below shows the argand diagram for 1 + i
1 + i becomes (1,1)
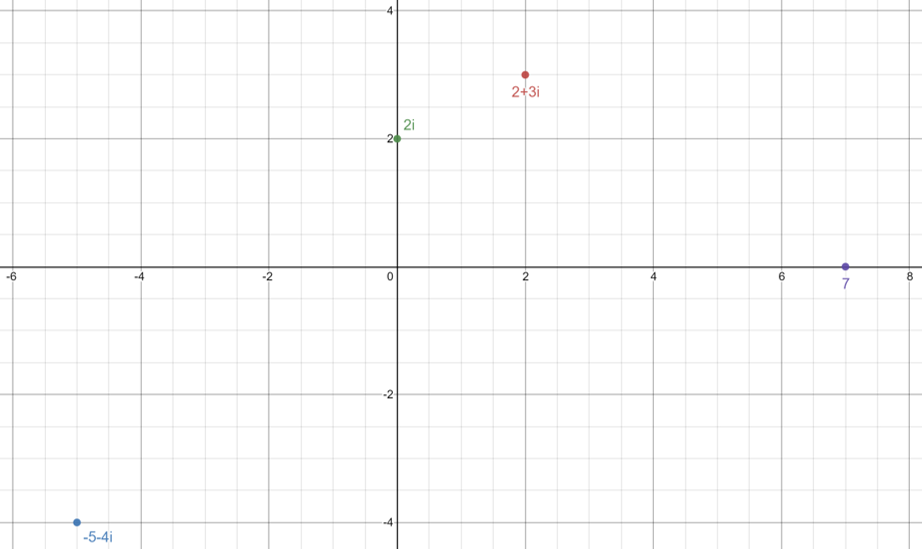
We can plot multiple complex numbers on the same argand diagram to see how they are plotted depending on there value:
2 + 3i becomes (2,3)
-5 - 4i becomes (-5,-4)
2i becomes (0,2)
7 becomes (7,0)
We can also plot the complex conjugate on an argand diagram to easily see the relationship between the two as well as a negative of both to see how they all relate
An example below shows where A = (2,-3)
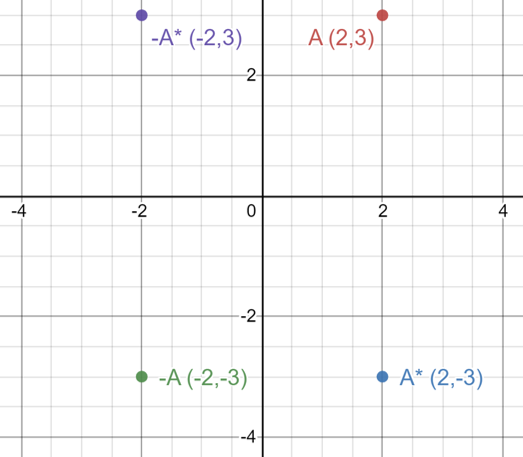
As we can see from the graph the complex conjugate of A is just a reflection in the x-axis and the -A is a rotation of 180° for A
Polar Form
Using an argand diagram we can easily find the magnitude of a complex number we simply just need to find √(x² + y²)
e.g.If we have the complex number 2 + 3i then we simply do:
r = √(2² + 3²) = √(4 + 9) = √13
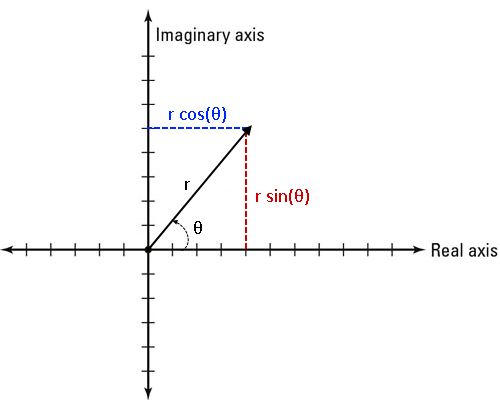
To find the angle between x and y we use trigonometry (SOH CAH TOA) as we know the length of x and y is equal to the real and imaginary part of the complex number
The magnitude is equal to r so we know all the lengths meaning we can create the equations:
sinθ = y/r
cosθ = x/r
tanθ = y/x
We can the rearrange the top two equations to understand that:
y = rsinθ
x = rcosθ
Inputting this into the equation for a complex number:
z = x + iy
z = r(cosθ) + r(isinθ)
z = r(cosθ + isinθ)
If we have the complex number z = 2 + 4i then we can use an argand diagram to plot this such as the one below:
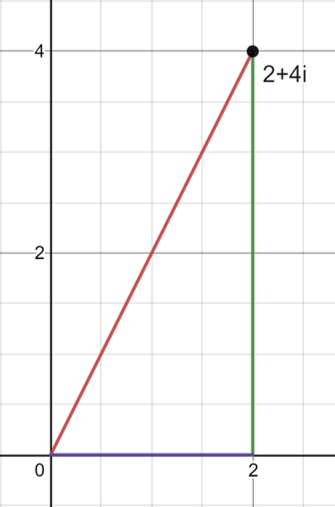
From this we know that the values:
x = 2
y = 4
r = √(2² + 4²) = √(4+16) = √20
Using the trigonometry shown above we can find θ using the equation:
tanθ = 4/2
θ = arctan(4/2) also written as tan-1(4/2)
θ = 1.11 rad
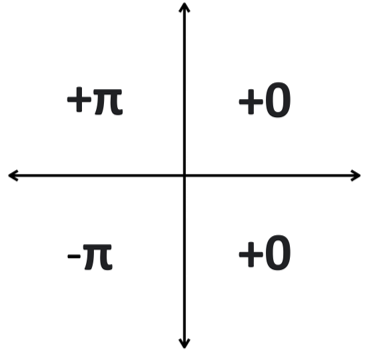
As this is in the top right quadrant we do not need to change the angle so we can continue and use the expression:
z = r(cosθ + isinθ)
z = √20 X[cos(1.11) + isin(1.11)]
This gives us the equation in a different form (Polar Form)
We can simplify how this looks into the expression:
r ∠ θ
We now find what our values were for r and θ and input them into this expression:
√20 ∠ 1.11 rad
We have now changed the expression into a simpler version of Polar form
Cartesian: z = 2 + 4i
Polar: z = √20 ∠ 1.11
Now we will do an example where we need to change the angle as the complex number is in a different quadrant such as:
-2 - i
First we need to plot this new complex number onto an argand diagram like the one below
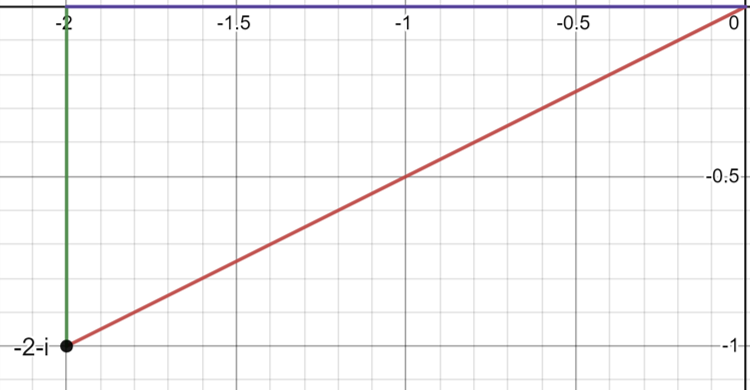
From this we know that the values:
x = -2
y = -1
r = √[(-2)² + (-1)²] = √(4+1) = √5
Using the trigonometry shown above we can find θ using the equation:
tanθ = (-1)/(-2) = 1/2
θ = arctan(1/2) also written as tan-1(1/2)
θ = 0.463 rad
We can clearly see however that this angle would put us in the quadrant as we should be expecting a negative angle as we are below the y = 0 line
Now we need to use the quadrants to see what we should do to this angle
The complex number is in the bottom left quadrant so we need to subtract π from our answer
θ = (0.463 - π) rad
θ = -2.68 rad
We can now see this is in the right quadrant meaning we now have the right angle so we can change this into Polar form
z = r(cosθ + isinθ)
z = √5 X [cos(-2.68)+ isin(-2.68)]
z = √5 X [cos(2.68)- isin(2.68)]
To express this in its simpler form we once again use:
z = r ∠ θ
z = √5 ∠ -2.68
This angle needs to be written as -2.68 even though we removed the negative in the other version by taking it out of the sin function it was originally a negative angle
Watch out for this in exams as if there is a negative sin inside the polar form that means the angle is negative and not positive as this is an easy mistake to make
We can change the sign of the sin die to these rules:
cos(-30) = cos(30)
sin(-30) = -sin(30)
This is because the cos wave is the same for both negative and positive values of θ where as the sin wave is flipped for negative and positive values as shown by the graph below
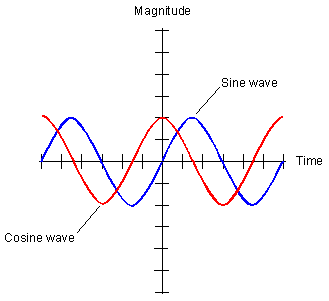
We therefore describe the cos wave as an even function as it is the same either side of 0\u00B0 where as the sine wave is called an odd function as each side has the reverse sign
Complex Conjugates
The reason we use Polar form is because it is much easier to multiply and divide complex numbers using it such as where:
z{1} = r{1} ∠ θ{1} and z{2} = r{2} ∠ θ{2}
z{1}z{2} = r{1}r{2} ∠ θ{1} + θ{2}
z{1}z{2} = r{1}r{2}(cos[θ{1} + θ{2}] + isin[θ{1} + θ{2}])
e.g z = 2 ∠ 1.43 and w = 1 ∠ 2.43
2X1 ∠ 1.43 + 2.43
2 ∠ 3.86
However as the angle is above π we must think about what quadrant it is in
This complex number would be in the bottom left quadrant meaning its value should lie between
-π and -π/2 howver we have 3.86
To solve this we subtract 2π from the angle as there are 2π in a rotation of a circle giving us:
3.86 - 2π = -2.42
This means our final answer is:
2 ∠ -2.42
Always check that your angle lies between π and -π
Now moving onto division we instead divide the magnitudes and subtract the angle like so:
z{1} = r{1} ∠ θ{1} and z{2} = r{2} ∠ θ{2}
z{1}/z{2} = r{1}/r{2} ∠ θ{1} - θ{2}
z{1}/z{2} = r{1}/r{2}(cos[θ{1} - θ{2}] + isin[θ{1} - θ{2}])
e.g z = 4 ∠ 2.52 and w = 2 ∠ 1.89
4/2 ∠ 2.52 - 1.89
2 ∠ 0.63
As you can see multiplying and dividing in Polar form is a lot easier than in Cartesian however unless stated in the exam you can use whichever method you find to be the easiest
Finally you can easily find the conjugate in Polar form simply by changing the sign of the angle such as:
z = r ∠ θ
z* = r ∠ -θ
e.g. z = 3 ∠ -2.13
Then z* = 3 ∠ 2.13