Changing Complex Forms

Information

We have already discussed how to change from Cartesian form (x+iy) to Polar form(r∠θ) but how do you change from Polar form to Cartesian form?
Lets start with an example where we have the Polar form:
z = 2[cos(7π/12) + isin(7π/12)]

First we check what quadrant the angle is in which we can easily do by drawing out the figure below:

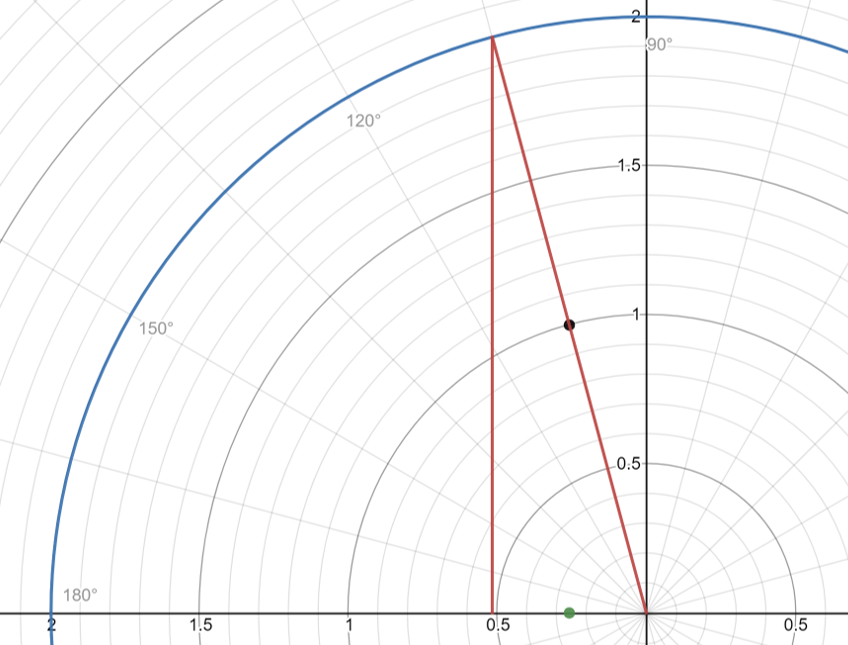
We can draw this graph as we know the radius is 2 and the angle is 7π/12
We can now clearly see that the complex number is locates in the upper left quadrant so we do not have the angle inside the triangle
To find this angle we take π and subtract the angle we have as π=180° and that is where the bottom of the triangle lies
(-π when in bottom left quadrant)

This means the angle is π - 7π/12 = 5π/12
Using the Polar coordinate equations we know:
sinθ = y/r
cosθ = x/r

As we know the angle and the radius we can now find x and y by rearranging to:
y = rsinθ
x = rcosθ

Filling these equations in gives us:
y = 2sin(5π/12) = 1.93
x = 2cos(5π/12) = 0.518

We now need to check the graph again to see if this is correct however we can see that we have a positive value for x when it is clearly a negative so all we need to do is flip the sign so our answer becomes:
z = -0.518 + 1.93i

Always check what quadrant the complex number is in as these are what you should be seeing:
Top Left:-x + iy
Top Right:x + iy
Bottom Right: x - iy
Bottom Left: -x - iy

Its easity just to put these Cartesian values into coordinates like this (x,iy) and you will easily know if you have the correct values

Geometry and Complex Numbers

By adding (a + ib) to any complex number will translate the point P(x,y) to point P'(x+a,y+b)
The length between two complex numbers (z and w) can be represented by:
|z - w|

The angle between the line made by the two complex numbers z and w and a line pparralel to the positive x axis can be represented by:
(z - w)

Circles:
Circles can be represented geometrically by the equation:
(x + a)² + (y + b)² = r²
Where Centre = (-a,-b) Radius = r

Example:

Sketch an Argand Diagram loci of the points for:
|z - 2i| = 4

First we need to remember that z = z + iy so we can replace the value of z in the equation with this substitute creating:
|x + iy + 2i| = 4
Secondly we need to collect the real and imaginary terms alike:
|x + i(y + 2)| = 4
From previous knowledge we know that the magnitude is equal to √(x²+y²) using this knowledge we can reconstruct the equation as:
√(x² + [y + 2]²) = 4
Next we need to expand the brackets such that:
√(x² + y² - 4y + 4) = 4
Squaring each side to remove the square root then gives us:
x² + y² - 4y + 4 = 16
We can then complete the square to get these values back into terms:
(x)² + (y-2)² - (-2)² +4 = 16
(x)² + (y-2)² = 16

Comparing this to the equation for a circle:
(x + a)² + (y + b)² = r²
Where Centre = (-a,-b) Radius = r

We find that:
a = 0
b = 2
r = √16 = 4
This means that the Centre = (0,2)

We then sketch the circle with this centre and radius like below:

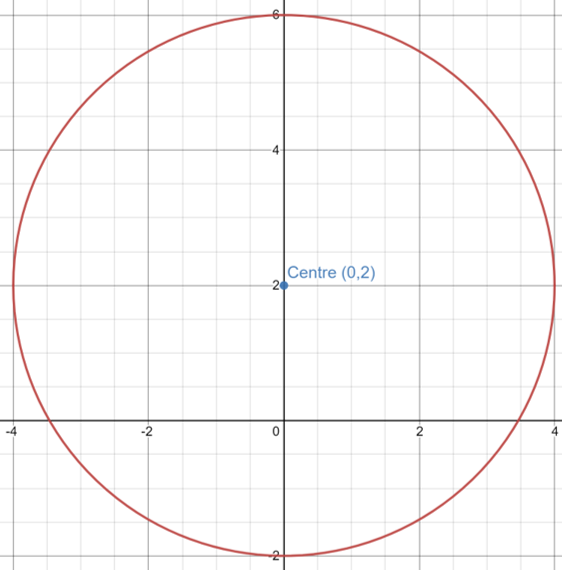
The complex number z is represented by the red circle as z can take any of these values as the distance from the point (0,2) to z is 4 therefore z lies on the circle centre (0,2) with radius 4

Example 2:
Sketch the Argand Diagram for the loci of points the satisfy:
|z - 2i| = |z + 6i|

Letting z = x + iy
|x + iy - 2i| = |x + iy + -6i|

We can now collect the real and imaginary parts and finding the magniitude of each we find:

Squaring both side so that all values are positve as any number squared is positive (except i):
(This means that we can remove the absolute vaslues as we know everything is positive)
x² + (y - 2)² = x² + (y + 6)²

Expanding the Brackets:
x² + y² -4y +4 = x² + y² + 12y + 36
-4y + 4 = 12y +36
-32 = 16y
y = -2

This means that wherever the value of y is eqaul to 2 the two complex numbers meet so we can now sketh the argand diagram wher
y = -2

z-i = 2(z+i)

Let z = x + iy
(x + iy) - i = 2(x + iy + i)

Squaring both sides:
x² + (y - 1)² = 2²[x² + (y + 1)²]

Expanding the Brackets:
x² + y² -2y + 1 = 4[x² + y² +2y + 1]
x² + y² -2y + 1 = 4x² + 4y² +8y + 4
3x² + 3y² +10y + 3 = 0

Dividing throughout by 3 so there are no coefficients on x² or y²
x² + y² +(10/3)y + 1 = 0

Now we can use completing the square to get the x and y terms into brackets:
(x)² + [y +(5/3)]² - (25/9) + 1 = 0
(x)² + [y +(5/3)]² - (16/9) = 0
(x)² + [y +(5/3)]² = (16/9)

Comparing this to the equation for a circle:
(x + a)² + (y + b)² = r²
a = 0
b = 5/3
r = √(16/9) = 4/3